Introduction to Random Strings solved by 5015

Modeling Random Genomes

We already know that the genome is not just a random strand of nucleotides; recall from “Finding a Motif in DNA” that motifs recur commonly across individuals and species. If a DNA motif occurs in many different organisms, then chances are good that it serves an important function.

At the same time, if you form a long enough DNA string, then you should theoretically be able to locate every possible short substring in the string. And genomes are very long; the human genome contains about 3.2 billion base pairs. As a result, when analyzing an unknown piece of DNA, we should try to ensure that a motif does not occur out of random chance.

To conclude whether motifs are random or not, we need to quantify the likelihood of finding a given motif randomly. If a motif occurs randomly with high probability, then how can we really compare two organisms to begin with? In other words, all very short DNA strings will appear randomly in a genome, and very few long strings will appear; what is the critical motif length at which we can throw out random chance and conclude that a motif appears in a genome for a reason?

In this problem, our first step toward understanding random occurrences of strings is to form a simple model for constructing genomes randomly. We will then apply this model to a somewhat simplified exercise: calculating the probability of a given motif occurring randomly at a fixed location in the genome.

Problem

Figure 1. The graph of the common logarithm function of x. For a given x-value, the corresponding y-value is the exponent to which we must raise 10 to obtain x. Note that x-values between 0 and 1 get mapped to y-values between -infinity and 0.

An array is a structure containing an ordered collection of objects (numbers, strings, other arrays, etc.). We let $A[k]$ denote the $k$-th value in array $A$. You may like to think of an array as simply a matrix having only one row.

A random string is constructed so that the probability of choosing each subsequent symbol is based on a fixed underlying symbol frequency.

GC-content offers us natural symbol frequencies for constructing random DNA strings. If the GC-content is $x$, then we set the symbol frequencies of C and G equal to $\frac{x}{2}$ and the symbol frequencies of A and T equal to $\frac{1-x}{2}$. For example, if the GC-content is 40%, then as we construct the string, the next symbol is 'G'/'C' with probability 0.2, and the next symbol is 'A'/'T' with probability 0.3.

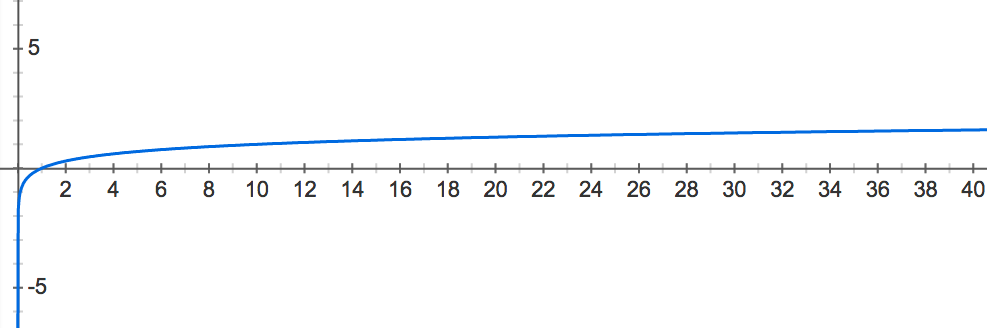
In practice, many probabilities wind up being very small. In order to work with small probabilities, we may plug them into a function that "blows them up" for the sake of comparison. Specifically, the common logarithm of $x$ (defined for $x > 0$ and denoted $\log_{10}(x)$) is the exponent to which we must raise 10 to obtain $x$.

See Figure 1 for a graph of the common logarithm function $y = \log_{10}(x)$. In this graph, we can see that the logarithm of $x$-values between 0 and 1 always winds up mapping to $y$-values between $-\infty$ and 0: $x$-values near 0 have logarithms close to $-\infty$, and $x$-values close to 1 have logarithms close to $0$. Thus, we will select the common logarithm as our function to "blow up" small probability values for comparison.

Given: A DNA string $s$ of length at most 100 bp and an array $A$ containing at most 20 numbers between 0 and 1.

Return: An array $B$ having the same length as $A$ in which $B[k]$ represents the common logarithm of the probability that a random string constructed with the GC-content found in $A[k]$ will match $s$ exactly.

Sample Dataset

ACGATACAA
0.129 0.287 0.423 0.476 0.641 0.742 0.783

Sample Output

-5.737 -5.217 -5.263 -5.360 -5.958 -6.628 -7.009

Hint

One property of the logarithm function is that for any positive numbers $x$ and $y$, $\log_{10}(x \cdot y) = \log_{10}(x) + \log_{10}(y)$.