Depth-first search readily identifies all the vertices of a graph that can be reached from a
designated starting point. It also finds explicit paths to these vertices, summarized in its
search tree.
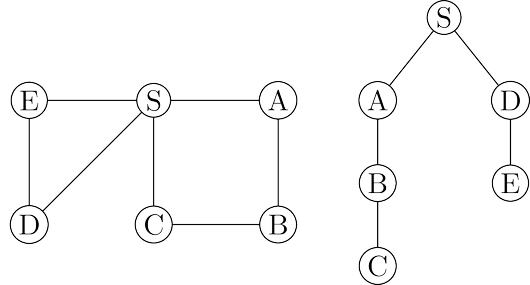
However, these paths might not be the most economical ones possible.
In the figure, vertex $C$ is reachable from $S$ by traversing just one edge, while the DFS tree
shows a path of length $3$.
Path lengths allow us to talk quantitatively about the extent to which different vertices of
a graph are separated from each other:
The distance between two nodes is the length of the shortest path between them.
To get a concrete feel for this notion, consider a physical realization of a graph that has a ball
for each vertex and a piece of string for each edge. If you lift the ball for vertex
$S$ high enough,
the other balls that get pulled up along with it are precisely the vertices reachable from
$S$.
And to find their distances from
$S$, you need only measure how far below
$S$ they hang.
For example, in figure below vertex $B$ is at distance $2$ from $S$, and there are two shortest
paths to it. When $S$ is held up, the strings along each of these paths become taut. On the
other hand, edge $(D, E)$ plays no role in any shortest path and therefore remains slack.
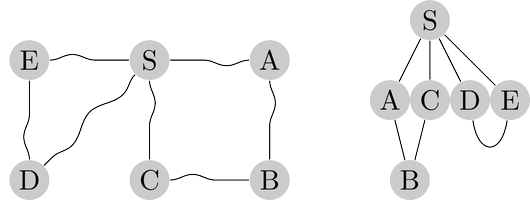
The lifting of $S$ partitions the graph into layers: $S$ itself, the nodes at distance
$1$ from it, the nodes at distance $2$ from it, and so on. A convenient way to compute distances
from $S$ to the other vertices is to proceed layer by layer. Once we have picked out the nodes
at distance $0, 1, 2, \dots , d$, the ones at $d + 1$ are easily determined: they are precisely the
as-yet-unseen nodes that are adjacent to the layer at distance $d$. This suggests an iterative algorithm
in which two layers are active at any given time: some layer $d$, which has been fully identified,
and $d + 1$, which is being discovered by scanning the neighbors of layer $d$.
Breadth-first search (BFS) directly implements this simple reasoning.
Initially the queue $Q$ consists only of $s$, the one node at distance $0$. And for each subsequent
distance $d = 1, 2, 3, \dots$, there is a point in time at which $Q$ contains all the nodes at distance
$d$ and nothing else. As these nodes are processed (ejected off the front of the queue), their
as-yet-unseen neighbors are injected into the end of the queue.

Let’s try out this algorithm on our earlier example to confirm that it does the
right thing. If $S$ is the starting point and the nodes are ordered alphabetically, they get visited
in the sequence shown in figure below.
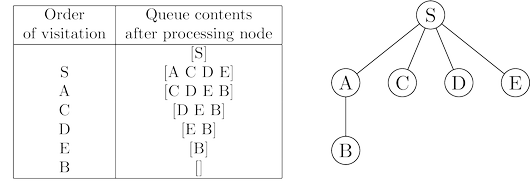
The breadth-first search tree, on the right, contains the
edges through which each node is initially discovered. Unlike the DFS tree, it
has the property that all its paths from $S$ are the shortest possible. It is therefore a
shortest-path tree.
Correctness and efficiency
We have developed the basic intuition behind breadth-first search. In order to check that
the algorithm works correctly, we need to make sure that it faithfully executes this intuition.
What we expect, precisely, is that
For each $d = 0, 1, 2, \dots$, there is a moment at which (1) all nodes at distance $\le d$
from $s$ have their distances correctly set; (2) all other nodes have their distances
set to $\infty$; and (3) the queue contains exactly the nodes at distance $d$.
This has been phrased with an inductive argument in mind. We have already discussed both
the base case and the inductive step. Can you fill in the details?
The overall running time of this algorithm is linear, $O(|V | + |E|)$, for exactly the same
reasons as depth-first search. Each vertex is put on the queue exactly once, when it is first
encountered, so there are $2 |V |$ queue operations. The rest of the work is done in the algorithm’s
innermost loop. Over the course of execution, this loop looks at each edge once (in directed
graphs) or twice (in undirected graphs), and therefore takes $O(|E|)$ time.
Source: Algorithms by Dasgupta, Papadimitriou, Vazirani. McGraw-Hill. 2006.



