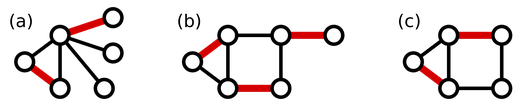
A maximum matching in a graph is a matching in that graph that contains at least as many nodes as any other possible matching. Because a perfect matching contains every node in a graph, perfect matchings are always maximum matchings by definition; however, although every graph will contain (at least one) maximum matching, only some graphs possess perfect matchings.
The figure below illustrates different maximum matchings (shown in red) from three different graphs. Note that none of these graphs has a perfect matching.
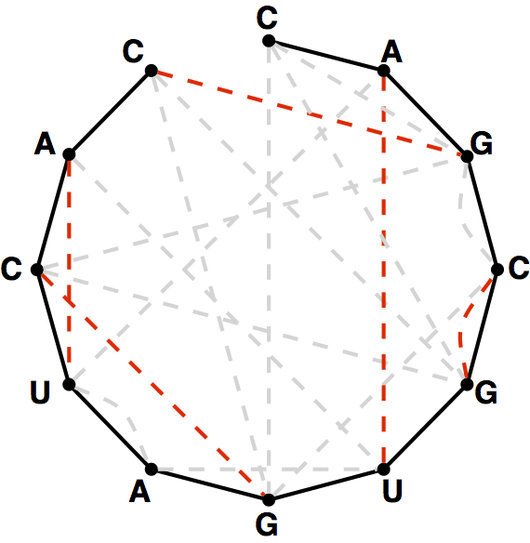
A maximum matching of basepair edges in a bonding graph corresponding to an RNA string