Wobble Bonding and RNA Secondary Structures solved by 658

Don't Look Down

We have discussed the problem of counting RNA secondary structures in previous problems. In this problem, we will add some assumptions to those used in “Motzkin Numbers and RNA Secondary Structures” to provide ourselves with an ultimately robust way of counting feasible RNA secondary structures.

First, in addition to the classic Watson and Crick base pairing of adenine with uracil and cytosine with guanine, uracil sometimes bonds with guanine, forming what is called a wobble base pair. As a result, we would like to allow wobble base pairing.

Second, although RNA folds over itself during base pairing, the structure of the molecule is rigid enough to prevent bases located very close to each other on the strand from bonding to each other.

Problem

Figure 1. A valid matching of basepair edges in the bonding graph of an RNA string, followed by a diagram of how this bonding will induce the resulting folded RNA.

Figure 2. All 12 possible valid basepair matchings in the bonding graph corresponding to the string s = CGAUGCUAG (including the trivial matching in which no edges are matched.) Courtesy Brian Tjaden.

Given an RNA string $s$, we will augment the bonding graph of $s$ by adding basepair edges connecting all occurrences of 'U' to all occurrences of 'G' in order to represent possible wobble base pairs.

We say that a matching in the bonding graph for $s$ is valid if it is noncrossing (to prevent pseudoknots) and has the property that a basepair edge in the matching cannot connect symbols $s_j$ and $s_k$ unless $k \geq j+4$ (to prevent nearby nucleotides from base pairing).

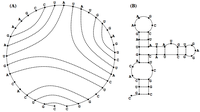
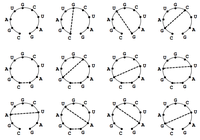
See Figure 1 for an example of a valid matching if we allow wobble base pairs. In this problem, we will wish to count all possible valid matchings in a given bonding graph; see Figure 2 for all possible valid matchings in a small bonding graph, assuming that we allow wobble base pairing.

Given: An RNA string $s$ (of length at most 200 bp).

Return: The total number of distinct valid matchings of basepair edges in the bonding graph of $s$. Assume that wobble base pairing is allowed.

Sample Dataset

AUGCUAGUACGGAGCGAGUCUAGCGAGCGAUGUCGUGAGUACUAUAUAUGCGCAUAAGCCACGU

Sample Output

284850219977421