Problem

A partition procedure is an essential part of the Quick Sort algorithm, the subject of one of the following problems. Its main goal is to put the first element of a given array to its proper place in a sorted array. It can be implemented in linear time, by a single scan of a given array. Moreover, it is not hard to come up with an in-place algorithm.

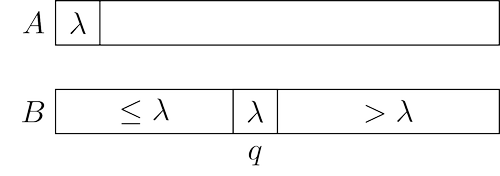
Given: A positive integer $n \le 10^5$ and an array $A[1..n]$ of integers from $-10^5$ to $10^5$.

Return: A permuted array $B[1..n]$ such that it is a permutation of $A$ and there is an index $1 \le q \le n$ such that $B[i] \le A[1]$ for all $1 \le i \le q-1$, $B[q]=A[1]$, and $B[i] > A[1]$ for all $q+1 \le i \le n$.

Sample Dataset

9
7 2 5 6 1 3 9 4 8

Sample Output

5 6 3 4 1 2 7 9 8