Insertion Sort solved by 2665

Computing the number of swaps in insertion sort

Insertion sort is a simple sorting algorithm that builds the final sorted array one item at a time. It is much less efficient on large lists than more advanced algorithms such as “Quick Sort”, “Heap Sort”, or “Merge Sort”. However, insertion sort provides several advantages: simple implementation, efficient for (quite) small data sets, $O(1)$ extra space.

When humans manually sort something (for example, a deck of playing cards), most use a method that is similar to insertion sort.

Source: Wikipedia

Although it is one of the elementary sorting algorithms with $O(n^2)$ worst-case time, insertion sort is the algorithm of choice either when the data is nearly sorted (because it is adaptive) or when the problem size is small (because it has low overhead).

For these reasons, and because it is also stable, insertion sort is often used as the recursive base case (when the problem size is small) for higher overhead divide-and-conquer sorting algorithms, such as “Merge Sort” or “Quick Sort”.

Visualization by David R. Martin: http://www.sorting-algorithms.com/insertion-sort

Problem

Insertion sort is a simple algorithm with quadratic running time that builds the final sorted array one item at a time.

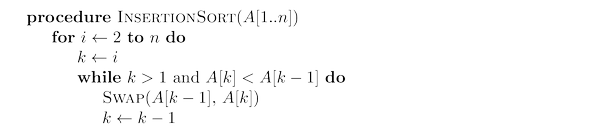
Given: A positive integer $n \le 10^3$ and an array $A[1..n]$ of integers.

Return: The number of swaps performed by insertion sort algorithm on $A[1..n]$.

Sample Dataset

6
6 10 4 5 1 2

Sample Output

12

Discussion

For this problem, it is enough to implement the pseudocode above with a quadratic running time and to count the number of swaps performed. Note however that there exists an algorithm counting the number of swaps in $O(n \log n)$.

Note also that Insertion Sort is an in-place algorithm as it only requires storing a few counters.