Generate the Convolution of a Spectrum solved by 508

Figure 1. Spectral convolution for the theoretical spectrum of NQEL. The most frequent elements in the convolution between 57 and 200 are (multiplicities in parentheses): 113 (8), 114 (8), 128 (8), 129 (8).

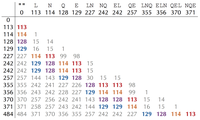
We define the convolution of a cyclic spectrum by taking all positive differences of masses in the spectrum. Figure 1 shows the convolution of the theoretical spectrum of "NQEL".

As predicted, some of the values in Figure 2.12 appear more frequently than others. For example, 113 (the mass of "L") appears eight times in the convolution of the theoretical spectrum of "NQEL"; we say that 113 has multiplicity 8. Six of the eight occurrences of 113 correspond to subpeptide pairs differing in an "L": "L" and ""; "LN" and "N"; "EL" and "E"; "LNQ" and "NQ"; "QEL" and "QE"; "NQEL" and "NQE".

Spectral Convolution Problem

Compute the convolution of a spectrum.

Given: A collection of integers Spectrum.

Return: The list of elements in the convolution of Spectrum in decreasing order of their multiplicities. If an element has multiplicity k, it should appear exactly k times.

Sample Dataset

0 137 186 323

Sample Output

137 137 186 186 323 49

Extra Dataset

Click for an extra dataset