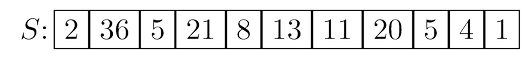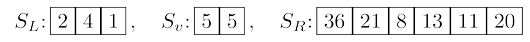The median of a list of numbers is its 50th percentile: half the numbers are bigger than it,
and half are smaller. For instance, the median of $[45, 1, 10, 30, 25]$ is $25$, since this is the middle
element when the numbers are arranged in order. If the list has even length, there are two
choices for what the middle element could be, in which case we pick the smaller of the two,
say.
The purpose of the median is to summarize a set of numbers by a single, typical value.
The mean, or average, is also very commonly used for this, but the median is in a sense more
typical of the data: it is always one of the data values, unlike the mean, and it is less sensitive
to outliers. For instance, the median of a list of a hundred $1$’s is (rightly) $1$, as is the mean.
However, if just one of these numbers gets accidentally corrupted to $10,000$, the mean shoots
up above $100$, while the median is unaffected.
Computing the median of $n$ numbers is easy: just sort them. The drawback is that this
takes $O(n \log n)$ time, whereas we would ideally like something linear. We have reason to be
hopeful, because sorting is doing far more work than we really need—we just want the middle
element and don’t care about the relative ordering of the rest of them.
When looking for a recursive solution, it is paradoxically often easier to work with a more
general version of the problem—for the simple reason that this gives a more powerful step to
recurse upon. In our case, the generalization we will consider is selection:
Input: A list of numbers $S$; an integer $k$.
Output: The $k$th smallest element of $S$.
For instance, if $k = 1$, the minimum of $S$ is sought, whereas if $k = \lceil |S|/2 \rceil $, it is the median.
A randomized divide-and-conquer algorithm for selection
Here’s a divide-and-conquer approach to selection. For any number $v$, imagine splitting list $S$
into three categories: elements smaller than $v$, those equal to $v$ (there might be duplicates),
and those greater than $v$. Call these $S_L$, $S_v$, and $S_R$ respectively. For instance, if the array
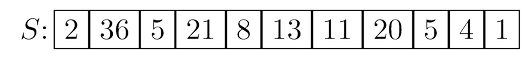
is split on $v = 5$, the three subarrays generated are
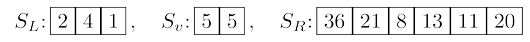
The search can instantly be narrowed down to one of these sublists. If we want, say, the
eighth-smallest element of $S$, we know it must be the third-smallest element of $S_R$ since
$|S_L| + |S_v| = 5$. That is, $\textrm{selection}(S, 8) = \textrm{selection}(S_R , 3)$. More generally, by checking k
against the sizes of the subarrays, we can quickly determine which of them holds the desired
element:
$$\text{selection}(S,k)=
\begin{cases}
\textrm{selection}(S_L,k) &\textrm{if } k \le |S_L| \\
v &\textrm{if } |S_L| < k \le |S_L|+|S_v| \\
\textrm{selection}(S_R,k-|S_L|-|S_v|) &\textrm{if } k>|S_L|+|S_v| \, .\\
\end{cases}
$$
The three sublists $S_L$, $S_v$, and $S_R$ can be computed from $S$ in linear time; in fact,
this computation can even be done in place, that is, without allocating new memory. We
then recurse on the appropriate sublist. The effect of the split is thus to shrink the number of
elements from $|S|$ to at most $\max\{|S_L|, |S_R|\}$.
Our divide-and-conquer algorithm for selection is now fully specified, except for the crucial
detail of how to choose $v$. It should be picked quickly, and it should shrink the array
substantially, the ideal situation being $|S_L|, |S_R| \approx |S|/2$. If we could always guarantee this situation,
we would get a running time of
$$T (n) = T (n/2) + O(n),$$
which is linear as desired. But this requires picking $v$ to be the median, which is our ultimate
goal! Instead, we follow a much simpler alternative: we pick $v$ randomly from $S$.
Efficiency analysis
Naturally, the running time of our algorithm depends on the random choices of $v$. It is possible
that due to persistent bad luck we keep picking $v$ to be the largest element of the array (or the
smallest element), and thereby shrink the array by only one element each time. In the earlier
example, we might first pick $v = 36$, then $v = 21$, and so on. This worst-case scenario would
force our selection algorithm to perform
$$ n+(n-1)+\dots+n/2 = \Theta(n^2)$$
operations (when computing the median), but it is extremely unlikely to occur. Equally
unlikely is the best possible case we discussed before, in which each randomly chosen $v$ just
happens to split the array perfectly in half, resulting in a running time of $O(n)$. Where, in
this spectrum from $O(n)$ to $\Theta(n^2)$, does the average running time lie? Fortunately, it lies very
close to the best-case time.
Given that a randomly chosen $v$ has a $50\%$ chance of being good, how many $v$’s do we need
to pick on average before getting a good one? Here’s a more familiar reformulation.
Lemma On average a fair coin needs to be tossed two times before a “heads” is seen.
Proof. Let $E$ be the expected number of tosses before a heads is seen. We certainly need at
least one toss, and if it’s heads, we’re done. If it’s tails (which occurs with probability $1/2$), we
need to repeat. Hence $E = 1 + E/2$, which works out to $E = 2$. ∎
Therefore, after two split operations on average, the array will shrink to at most
three-fourths of its size. Letting $T (n)$ be the expected running time on an array of size $n$, we get
$$T (n) \le T (3n/4) + O(n).$$
This follows by taking expected values of both sides of the following statement:
Time taken on an array of size $n$ $≤$ (time taken on an array of size $3n/4$) $+$ (time to reduce array size to $\le 3n/4$),
and, for the right-hand side, using the familiar property that the expectation of the sum is the
sum of the expectations.
From this recurrence we conclude that $T (n) = O(n)$: on any input, our algorithm returns
the correct answer after a linear number of steps, on the average.
Source: Algorithms by Dasgupta, Papadimitriou, Vazirani. McGraw-Hill. 2006.