Glossary

For a collection of strings formed over the same underlying alphabet, their trie (often pronounced "try" to avoid ambiguity) is a rooted tree formed by the following process. For every unique first symbol in the strings, an edge is formed connecting the root to a new vertex. This symbol is then used to label the edge.

We then iterate the process by moving down one level. Say that an edge connecting the root to node $v$ is labeled with 'A'; then we delete the first symbol from every string in the collection beginning with 'A' and then start the process again, treating $v$ as our root. We apply this procedure to all nodes that are adjacent to the root. See the figure below for a trie on the strings "apple", "apropos", "banana", "bandana", and "orange".

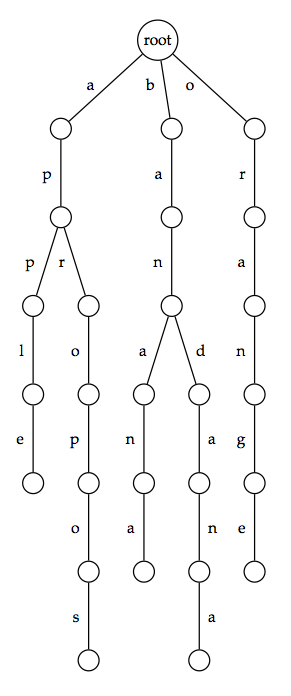
As a result of this method, the symbols along the edges of any path from the root to a leaf will spell out a unique string from the collection, and vice-versa: any path from the root to a leaf will correspond to a string. The only exception to this rule arises when one string in the collection is a prefix of another (this would cause the first string to be encoded as a path terminating at an internal node). Because the underlying strings in the collection are typically not short, this extraneous case will usually not occur, and we will typically assume that it does not.

Tries are particularly useful in the problem of pattern matching, where they offer an efficient way of encoding the information contained in a collection of patterns.