An Eulerian cycle is a cycle in a graph that traverses every edge of the graph exactly once. The Eulerian cycle is named after Leonhard Euler, who first described the ideas of graph theory in 1735 in his solution of the Bridges of Konigsberg Problem.
This problem asked whether it was possible for a denizen of Konigsberg (which at the time was located in Prussia) to take a walk through the four parts of the city, crossing every bridge over the Pregel river, and return to one's starting point. The figure below contains a map of Konigsberg as it appeared in 1735; bridges are highlighted in blue, and each sector of the city (there are four: two river islands, as well as both banks of the river).
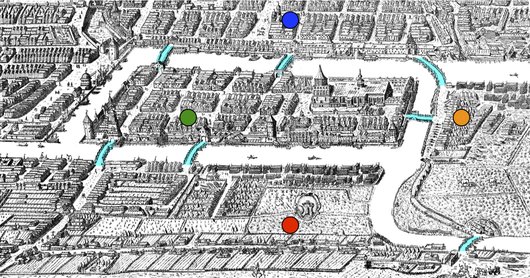
Euler's approach to the problem was to compress each area of the city to a node (as shown by the colored points in the map above), then draw each bridge as an edge connecting corresponding sectors of the city. The walk that the residents of Konigsberg desired would then correspond to an Eulerian cycle in this graph, which is shown below.
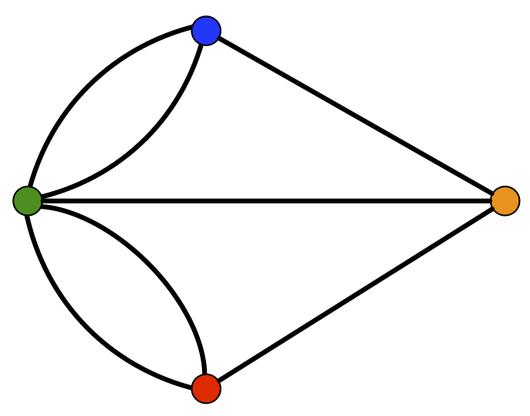
However, Euler demonstrated that a graph will possess an Eulerian cycle precisely when the degree of any node is even. As a result, the graph of Konigsberg fails to possess an Eulerian cycle, and so the desired walk cannot exist.
The graph below illustrates a graph in which every node has even degree, with an Eulerian cycle labeled by edges in order from "A" to "K". Note that this Eulerian cycle is not a simple cycle.

Eulerian cycles may also be defined on directed graphs; they are just directed cycles that traverse every edge in the graph exactly once (and traverse each directed edge from tail to head).