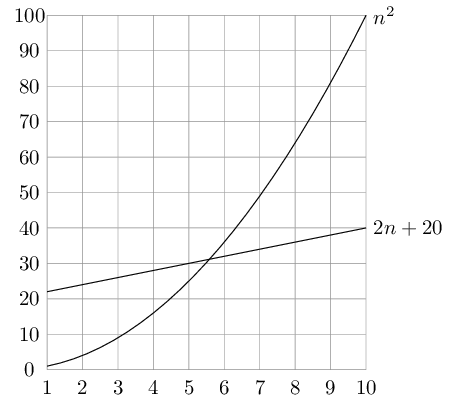
Figure 1
Saying $f = O(g)$ is a very loose analog of “$f \le g$.” It differs from the usual notion of $\le$
because of the constant $c$, so that for instance $10n = O(n)$. This constant also allows us to
disregard what happens for small values of $n$. For example, suppose we are choosing between
two algorithms for a particular computational task. One takes $f_1 (n) = n^2$ steps, while the
other takes $f_2(n) = 2n + 20$ steps (Figure 1). Which is better? Well, this depends on the
value of $n$. For $n \le 5$, $f_1$ is smaller; thereafter, $f_2$ is the clear winner. In this case, $f_2$ scales
much better as $n$ grows, and therefore it is superior.
This superiority is captured by the big-O notation: $f_2 = O(f_1)$, because
$$\frac{f_2(n)}{f_1{n}}=\frac{2n+20}{n^2} \le 22$$
or all $n$; on the other hand, $f_1 \neq O(f_2)$, since the ratio $f_1(n)/f_2(n) = n^2/(2n + 20)$ can get
arbitrarily large, and so no constant $c$ will make the definition work.
Now another algorithm comes along, one that uses $f_3 (n) = n + 1$ steps. Is this better
than $f_2$? Certainly, but only by a constant factor. The discrepancy between $f_2$ and $f_3$ is tiny
compared to the huge gap between $f_1$ and $f_2$. In order to stay focused on the big picture, we
treat functions as equivalent if they differ only by multiplicative constants.
Returning to the definition of big-O, we see that $f_2 = O(f_3)$:
$$\frac{f_2(n)}{f_3{n}}=\frac{2n+20}{n+1} \le 20\, ,$$
and of course $f_3 = O(f_2 )$, this time with $c = 1$.
Just as $O(\cdot)$ is an analog of $\le$, we can also define analogs of $\ge$ and $=$ as follows:
$$f = \Omega(g) \text{ means } g = O(f)$$
$$f = \Theta(g) \text{ means } f = O(g) \text{ and } f = \Omega(g) \, .$$
In the preceding example, $f_2 = \Theta(f_3)$ and $f_1 = \Omega(f_3)$.
Big-O notation lets us focus on the big picture. When faced with a complicated function
like $3n^2 + 4n + 5$, we just replace it with $O(f (n))$, where $f (n)$ is as simple as possible. In this
particular example we’d use $O(n^2)$, because the quadratic portion of the sum dominates the
rest. Here are some commonsense rules that help simplify functions by omitting dominated
terms:
- Multiplicative constants can be omitted: $14n^2$ becomes $n^2$.
- $n^a$ dominates $n^b$ if $a > b$: for instance, $n^2$ dominates $n$.
- Any exponential dominates any polynomial: $3^n$ dominates $n^5$ (it even dominates $2^n$).
- Likewise, any polynomial dominates any logarithm: $n$ dominates $(\log n)^3$. This also
means, for example, that $n^2$ dominates $n\log n$.
Don’t misunderstand this cavalier attitude toward constants. Programmers and algorithm
developers are very interested in constants and would gladly stay up nights in order to make
an algorithm run faster by a factor of $2$. But understanding algorithms at the basic level
would be impossible without the simplicity afforded by big-O notation.
Source: Algorithms by Dasgupta, Papadimitriou, Vazirani. McGraw-Hill. 2006.